Large Deviation Theory: Taming the Tails of Probability

Understanding the improbable events that shape our universe and beyond

Why Should We Care?

LDT isn’t just a theoretical curiosity. These rare, tail events can have huge impacts in many fields:

  • Finance & Economics: Modeling extreme market swings or systemic crashes.
  • Networking & Telecommunications: Predicting sudden traffic spikes and preventing network overloads.
  • Climate & Environmental Science: Assessing once-in-a-century floods, heatwaves, or other extreme weather.
  • Astrophysics & Cosmology: Spotting rare cosmic structures or extreme gravitational lensing signals that reveal new physics.

LDT in Action

At its core, LDT addresses the question: “How do probabilities of extreme deviations scale when I look at bigger (or more) systems?” For many distributions, the probability of large fluctuations shrinks exponentially with system size. LDT’s tools—like rate functions and scaling exponents—help us probe the structure of these tails and understand what truly drives outliers.

A handy example is summing random variables: while the Law of Large Numbers and Central Limit Theorem describe the bulk near the mean, LDT digs into how improbable it is for sums to be many standard deviations away from the mean, and how that improbability depends on the number of variables.

A Toy Demonstration: Coin Tosses

Suppose you toss a fair coin n times. Let k be the number of heads, so the rate of heads is k/n. The Binomial distribution describes the probability of exactly k heads: 

P(Heads = k) = ( n choose k ) * (1/2)^n

While this distribution might look bell-shaped for large n, the tails—far from k/n = 0.5—become exponentially suppressed. That’s precisely what Large Deviation Theory captures, providing a rate function for how quickly those probabilities drop off.

Visualizing It

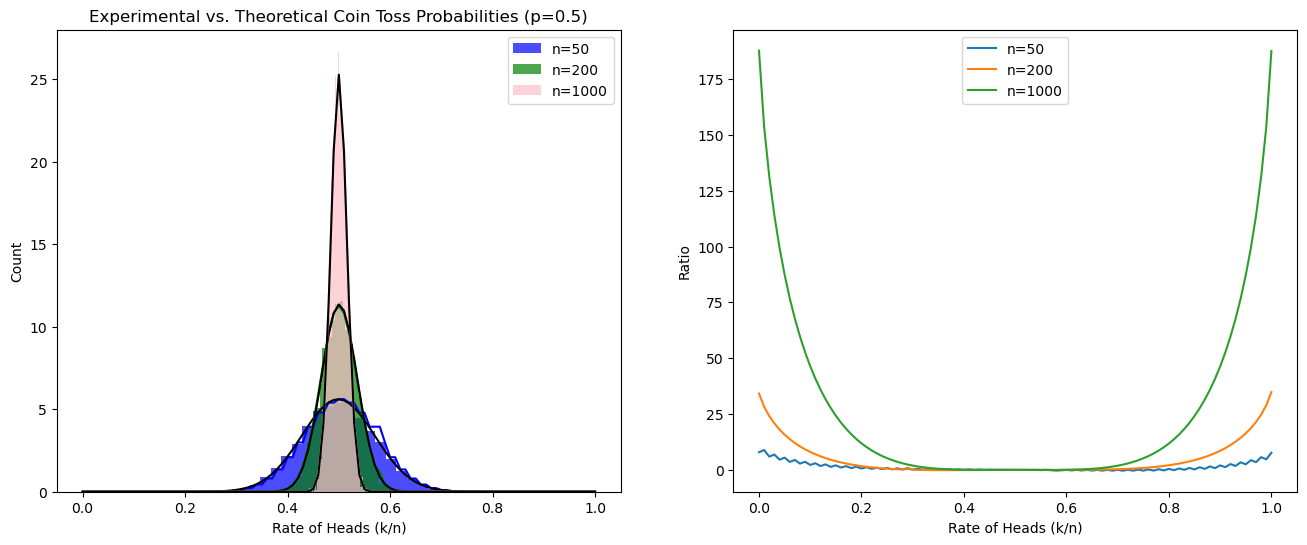
Coin Toss Distribution vs. Theory
Comparing empirical coin-toss data (histograms) with binomial and Gaussian approximations.

As n grows, the bulk of outcomes clusters near 0.5, but rare events—like 70% or 30% heads—shrink at a rate faster than the naive Gaussian tail might suggest.

Applications in Cosmology

  • Galaxy Clusters & Voids: Rarely massive clusters or giant cosmic voids can be highly sensitive to underlying physics.
  • Weak Lensing Signals: Improbable lensing configurations may expose dark matter distributions or anomalies hinting at new physics.
  • Cosmic Variance at the Edges: Large surveys push us to identify if extreme cosmic features are consistent with standard models or require new theories.

Conclusion

Large Deviation Theory offers a powerful lens to study the improbable events that—more often than we’d like—drastically shape our world and universe. From coin tosses to systemic financial crises to cosmic anomalies, LDT’s focus on probability tails enriches our understanding of complex systems. By grappling with these outliers—and quantifying just how “out there” they truly are—we uncover deeper insights into the nature of reality itself.