Theoretical wavelet ℓ₁-norm from one-point probability density function prediction
I'm incredibly happy to share that my first-author paper, "Theoretical wavelet ℓ₁-norm from one-point probability density function prediction", is now published in Astronomy & Astrophysics (Vol. 691, A80, 2024).
Some background, some thoughts
If you're in the world of weak gravitational lensing, you've probably heard about how much information we lose when we just stop at the power spectrum. Sure, it's great for Gaussian fields, but the Universe? She's a bit more complicated than that. And while we’ve long known that non-Gaussian features hold a treasure trove of cosmological information, actually capturing and modeling them is hard—especially without simulations.
Over the years, the wavelet ℓ₁-norm has shown up as a powerful statistic to probe non-Gaussianity. It’s simple, scale-aware, and surprisingly sensitive to structure. But up until now, it’s been more of an empirical tool—a cool trick that works, but one that lacked a theoretical backbone. That’s exactly what I wanted to change.
What I tried to do
I set out to build a theoretical model for the ℓ₁-norm of wavelet coefficients in convergence maps. The approach is rooted in large-deviation theory (LDT), which helps us predict the one-point probability density function (PDF) of the convergence field. From there, the core idea was this: if the wavelet transform acts like a difference of top-hat filters, and if we already know how to predict the PDF at different smoothing scales, then we can construct a prediction for the ℓ₁-norm analytically—**without any reliance on simulations**.
The ℓ₁-norm is, in essence, a measure of sparsity: the sum of absolute values of the wavelet coefficients at a given scale. It's beautiful in its simplicity and reflects how “peaky” or structured the field is. That structure changes with scale, and it changes with cosmology. And because we’re working in wavelet space, we preserve spatial information while separating features by scale—something that's especially useful for understanding how nonlinear structures grow and cluster.
How it compares with simulations
To see how well the theoretical prediction holds up, I tested it against simulated convergence maps from the Takahashi simulations. The agreement, especially in the weakly nonlinear regime, was much better than I had dared to expect.
ℓ₁-norm across wavelet scales
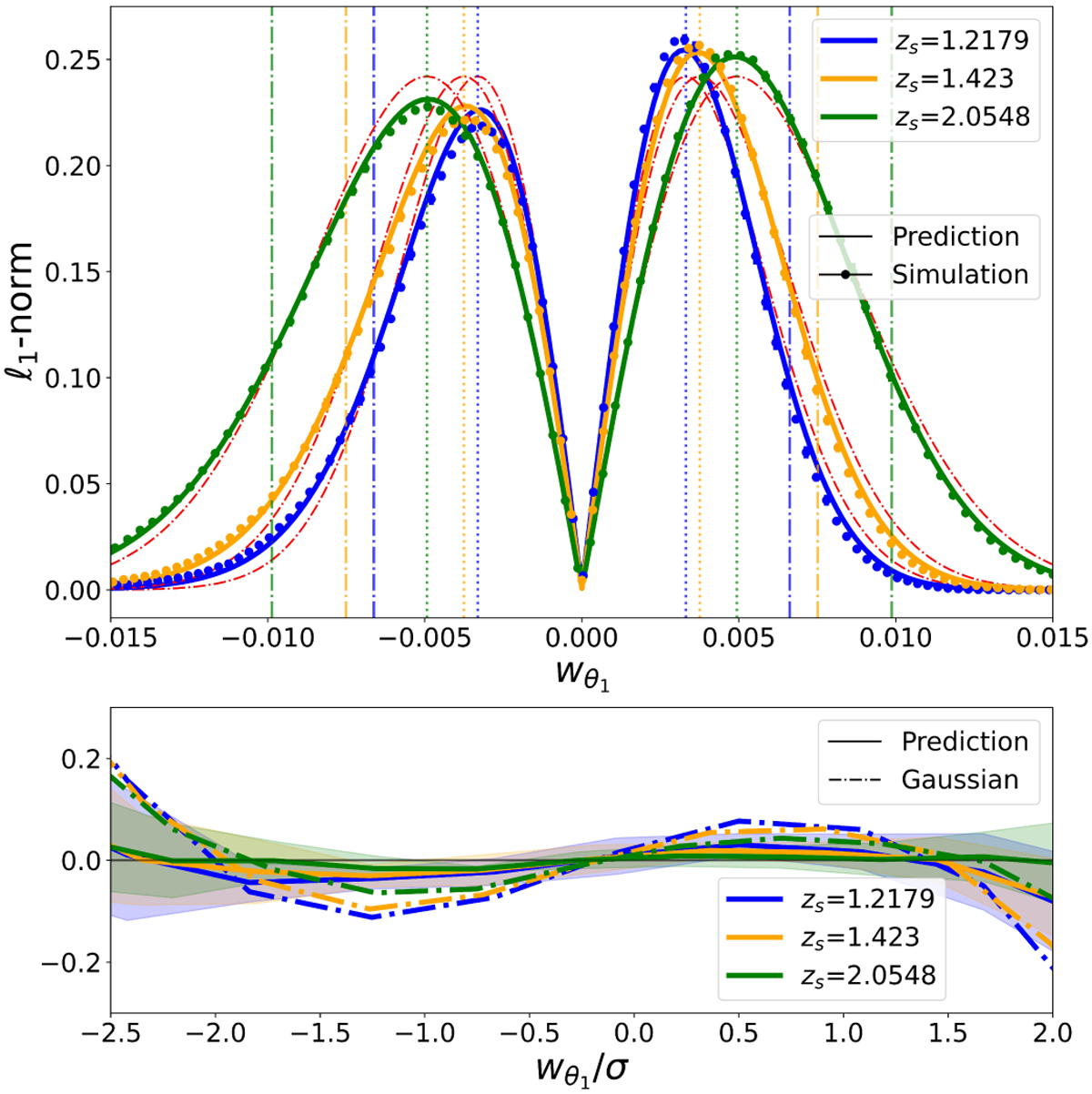
The shape, scale dependence, and amplitude of the ℓ₁-norm match theory and simulations very well. More than just a fit, this confirmed that the underlying PDF predictions—crafted through LDT—are capturing the real statistical behavior of the convergence field in this non-Gaussian regime.
Cosmology dependence: ∂ℓ₁/∂Ωₘ
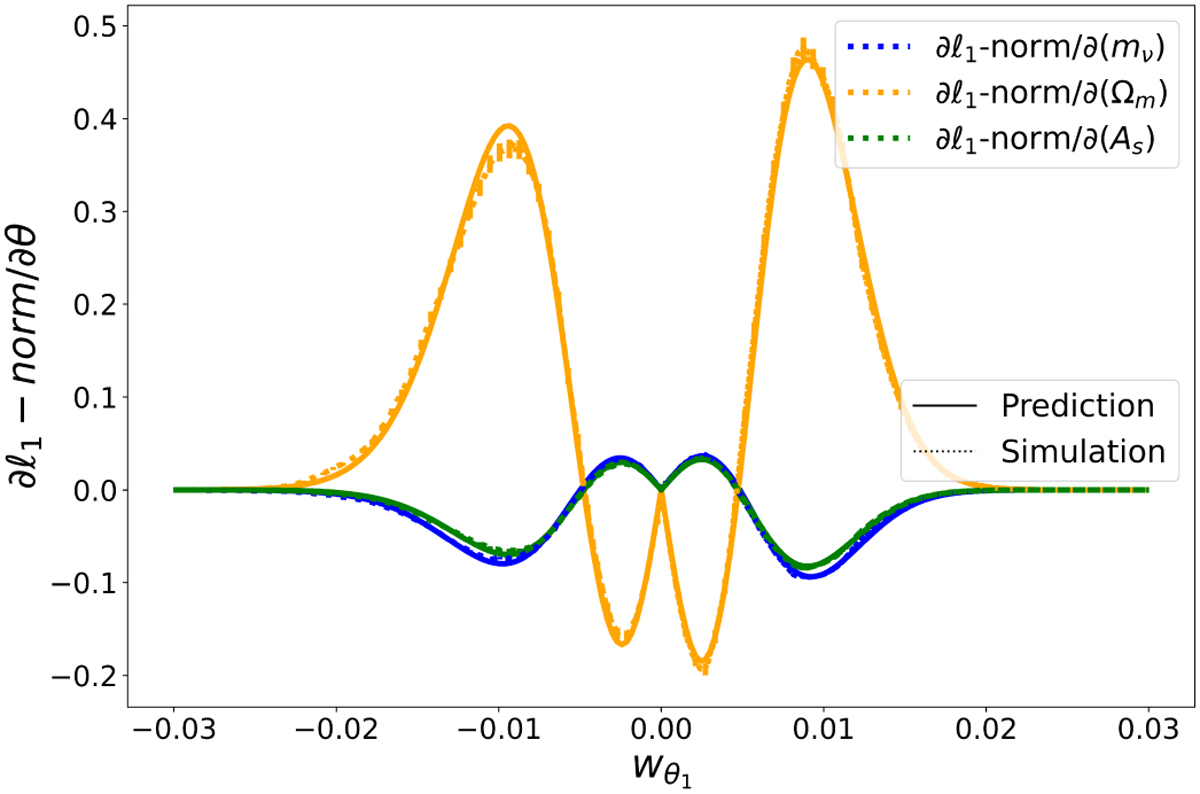
One of the most exciting parts was observing how the ℓ₁-norm responds to changes in cosmological parameters—like Ωₘ and σ₈. It clearly shifts with them, and the theory tracks that sensitivity. This makes it a promising candidate not just for summary statistics, but also for **likelihood-free inference** or emulator-based cosmological pipelines.
Why it matters (to me, and maybe to you too)
This work feels special because it brings together theory, computation, and a bit of intuition about structure in the Universe. It’s a step towards building tools that aren’t just empirically useful, but theoretically sound—tools that we can rely on when simulations become expensive, when data becomes vast, and when we want inference pipelines that scale.
It also quietly emphasizes the fact that we can do more with less. We don’t always need to simulate the entire cosmos to understand its fingerprints—we just need the right mathematical lens.
Code and Repository
All the code used in this work is available in my GitHub repository: 👉 WALE: Wavelet L1 Estimator
The repository includes:
- Scripts to compute the theoretical ℓ₁-norm from PDF predictions
- Wavelet decomposition and LDT tools
- Validation and comparison plots with simulations
- A modular interface for emulator-building
Takeaways
- Theoretical, simulation-free prediction of the wavelet ℓ₁-norm using LDT
- Accurate across multiple scales and cosmological models
- Captures sensitivity to Ωₘ and σ₈, ideal for inference pipelines
What’s next?
- Study impact of noise, masks, and observational systematics
- Apply the method to real lensing data
- Develop an emulator based on this theory for parameter inference
Read the paper
Theoretical wavelet ℓ₁-norm from one-point PDF prediction (A&A, 2024)