Generative modeling of convergence maps based on predicted one‑point statistics

I’m thrilled to share that my latest paper, “Generative modeling of convergence maps based on predicted one‑point statistics”, is now available on arXiv:2507.01707.

Why I wrote this

After building the theory for wavelet ℓ₁-norms, I kept wondering: could we go beyond predicting just one statistic? Could we generate entire convergence maps that match multiple statistical properties—**without relying on simulations**? This paper is an attempt to do just that.

The idea

Using the one-point PDF of the convergence field predicted from large-deviation theory (LDT), I developed a framework to reconstruct full convergence maps. The goal: create maps that simultaneously match a given power spectrum and the one-point PDF (and derived ℓ₁-norms) at different wavelet scales.

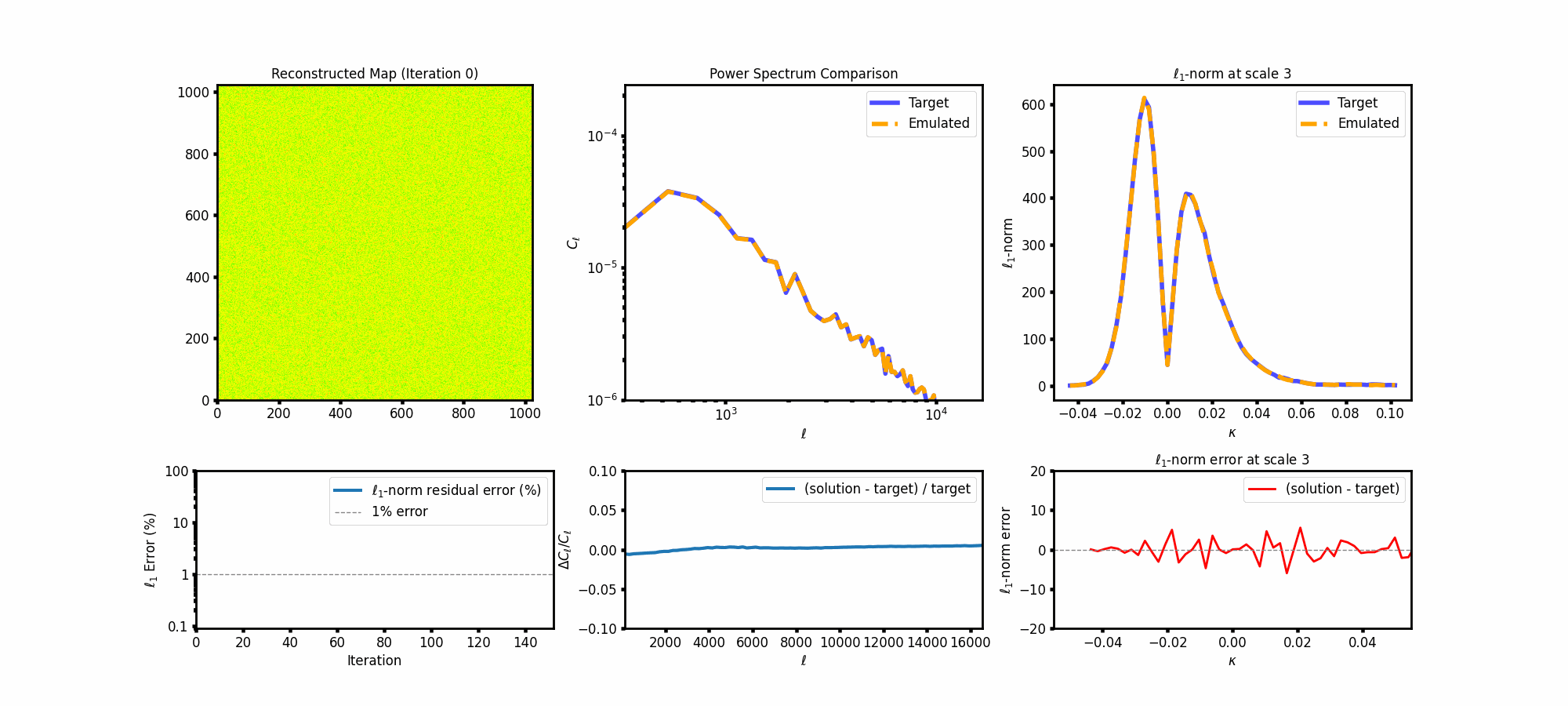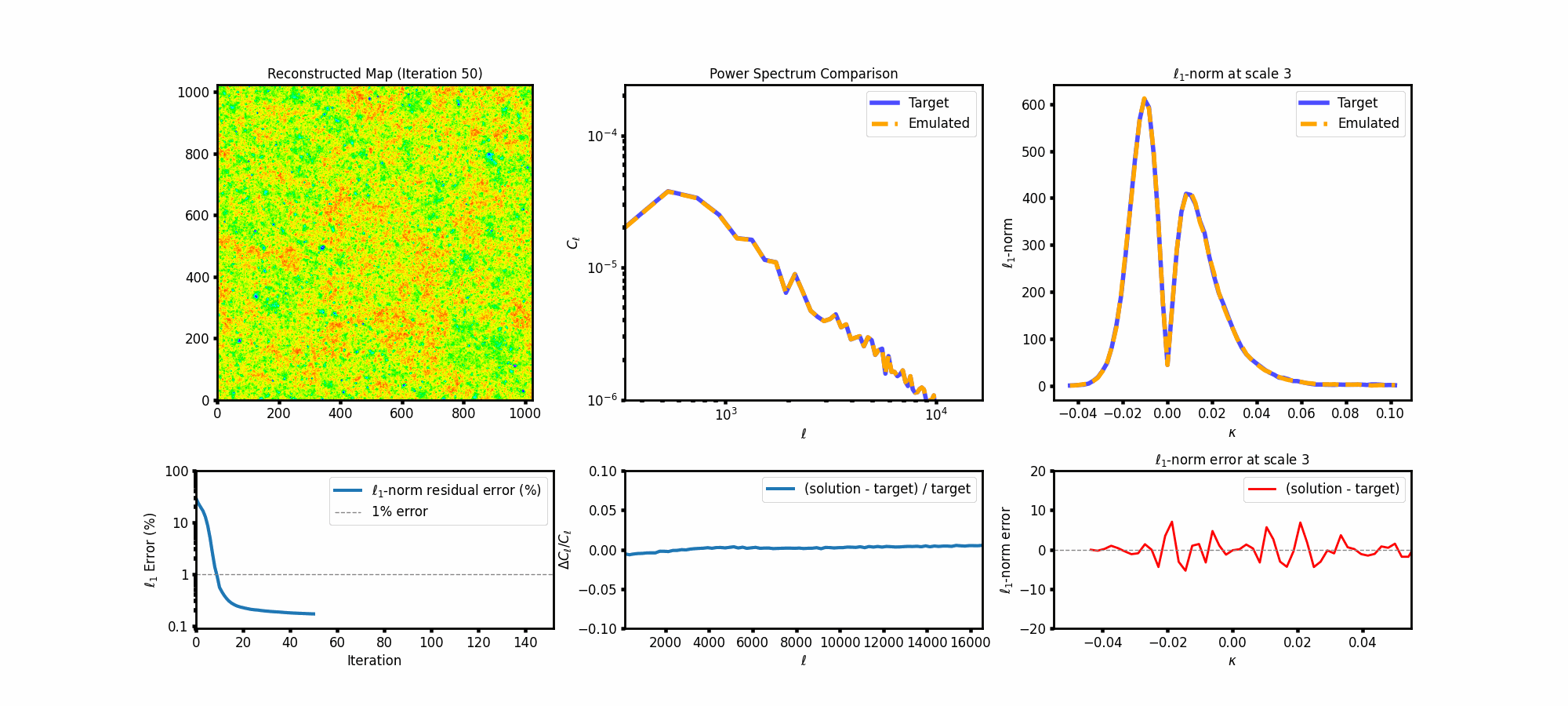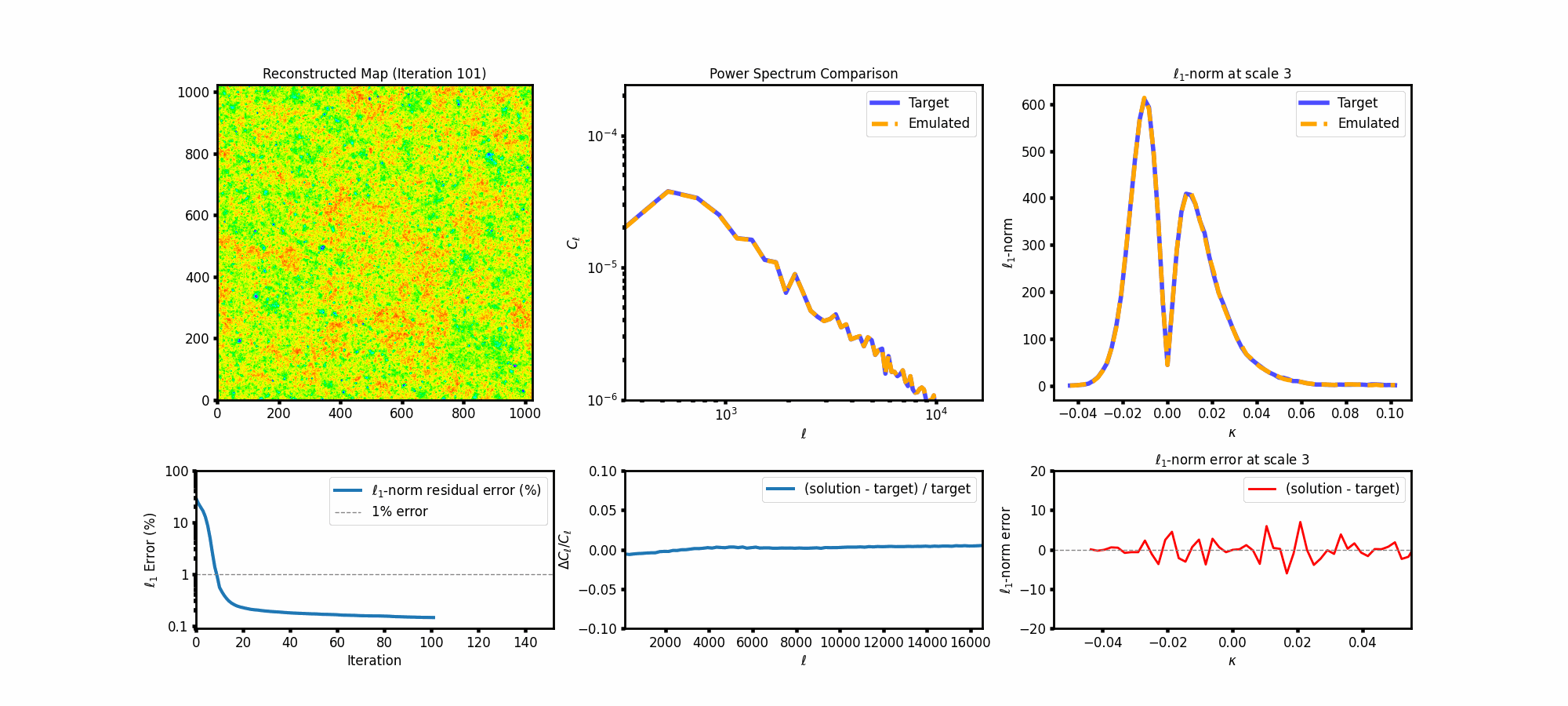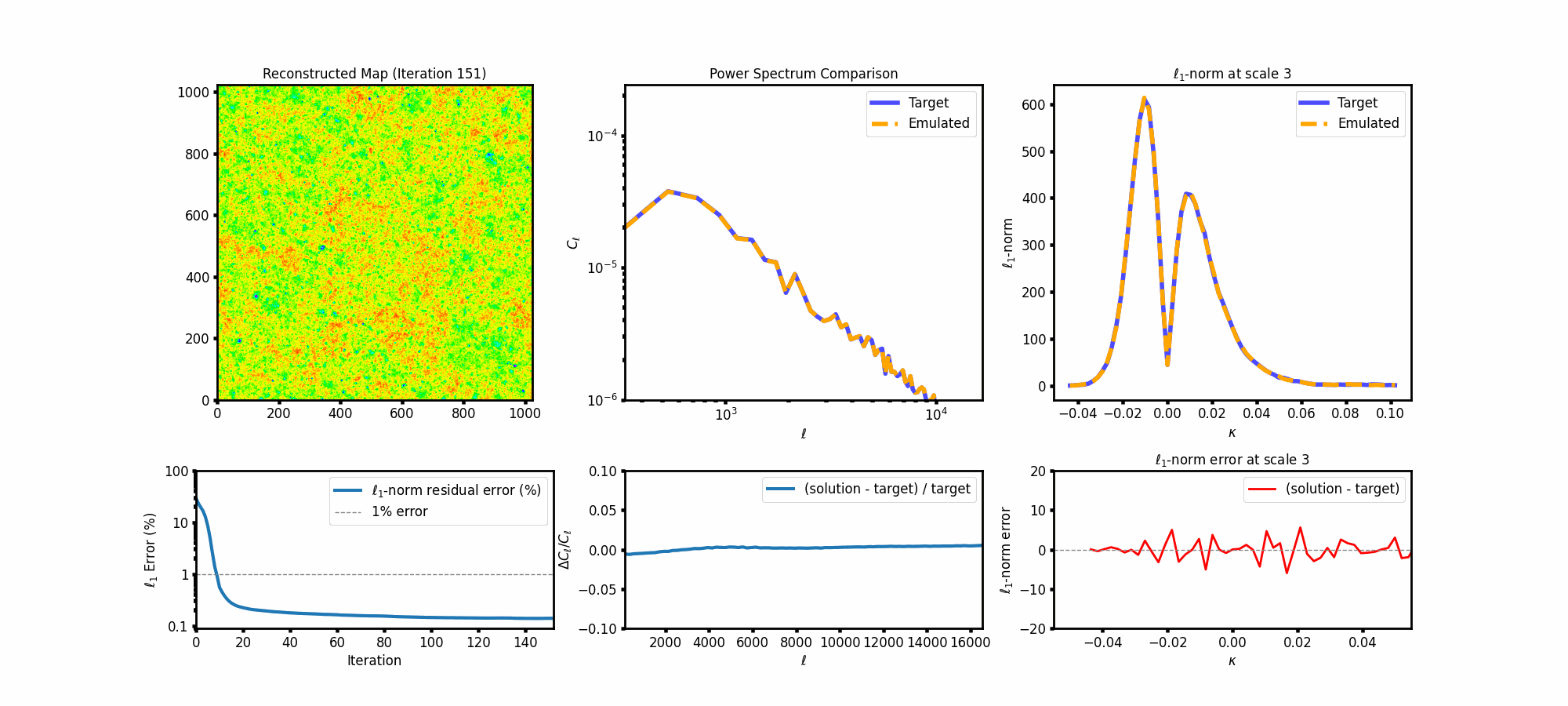
The reconstruction is iterative. Starting from a Gaussian random field, the map evolves step by step to match the target statistics. With each iteration, the map gets closer to the desired morphology, power spectrum, and ℓ₁ signature.

How the algorithm works

The reconstruction is based on a forward-backward method that alternates between enforcing two constraints: the power spectrum and the ℓ₁-norm at each wavelet scale. Starting from a random Gaussian field, we iteratively apply corrections in Fourier and wavelet space to nudge the map toward the target statistics.

Figure 2: Schematic of the forward-backward method. Each iteration applies corrections to enforce both the ℓ₁-norm and power spectrum, gradually transforming a random initial map into a realistic emulated map.

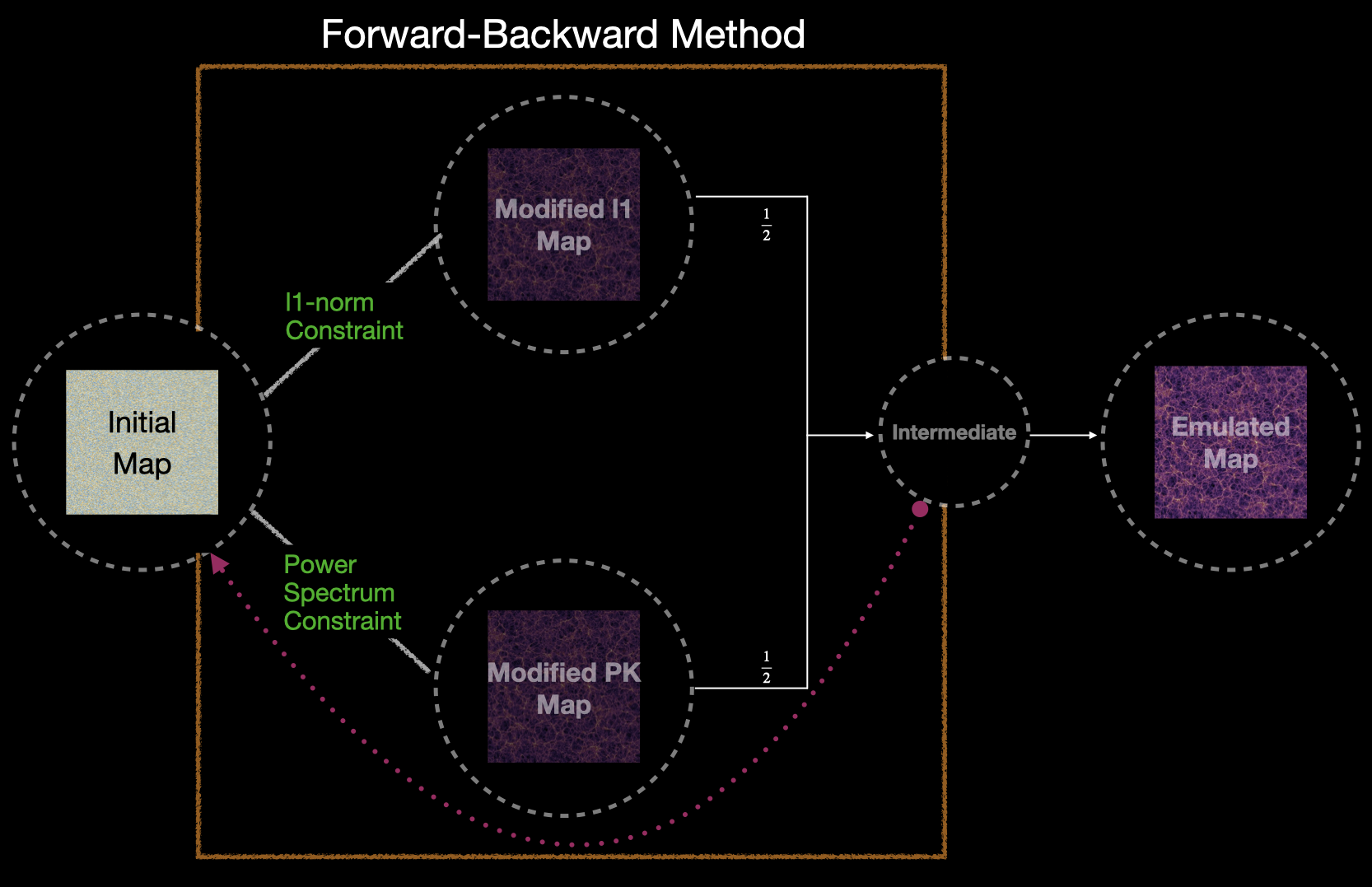
The intermediate updates from each constraint are combined and fed back into the loop, leading to stable convergence. This approach balances two different statistical domains: non-Gaussian features captured by the ℓ₁-norm and Gaussian structure captured by the power spectrum.

What it looks like

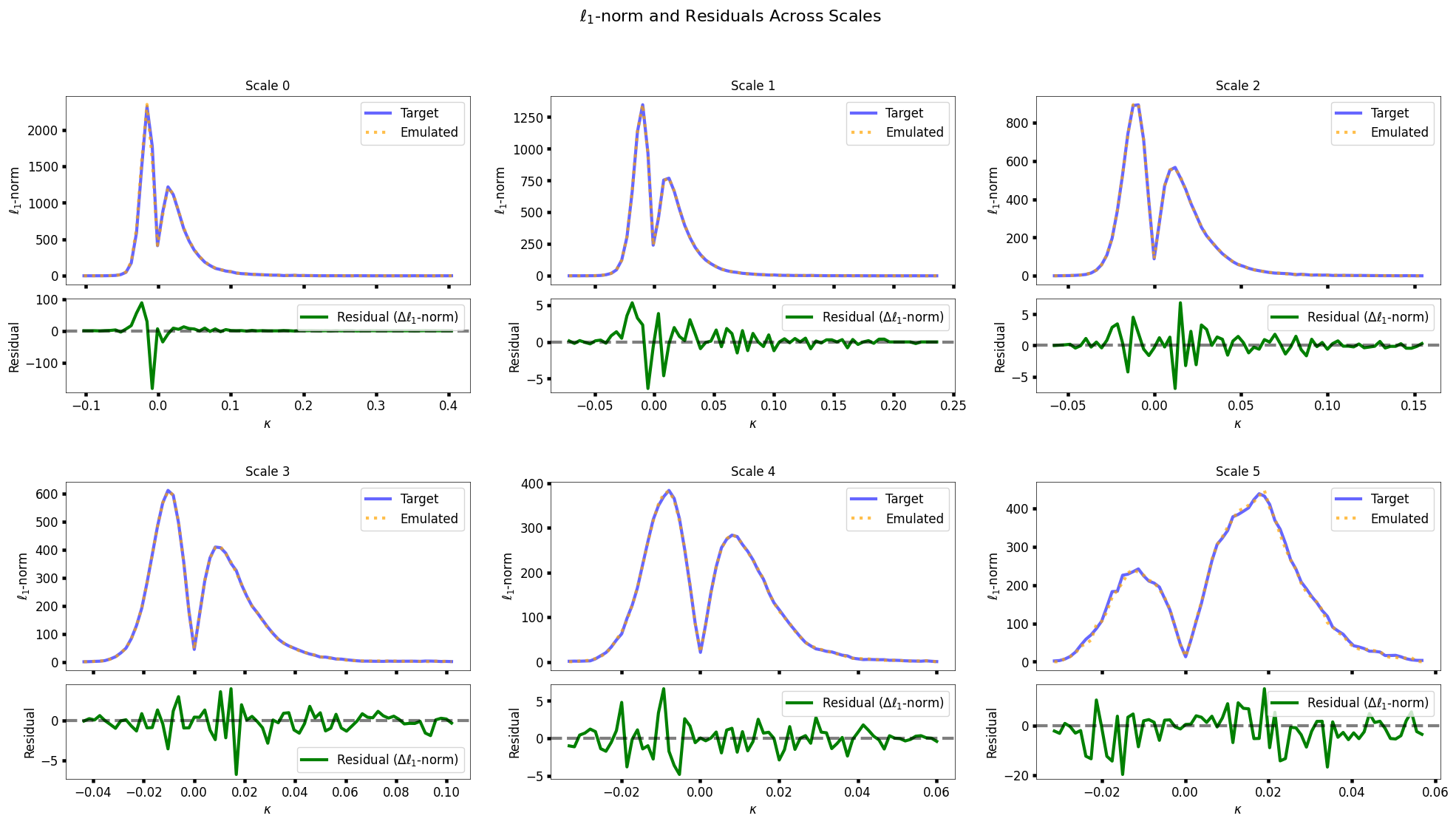
To dig deeper, here’s a figure showing how well the ℓ₁-norm distributions are matched across all wavelet scales. The blue curves are from the target statistics (based on theory), and the orange dashed lines represent the generated maps. The bottom panels for each scale show the residuals—i.e., the difference between emulated and target values.

Figure 5: ℓ₁-norm distributions (top) and residuals (bottom) across wavelet scales 0–5. The emulator captures both shape and amplitude with high accuracy.

The evolution (a little hypnotic)

Watching the map evolve is quite satisfying—especially as the power spectrum and ℓ₁-norm errors shrink with iteration. Here’s a GIF showing how the reconstruction progresses:

GIF: Evolution of the map, power spectrum, and ℓ₁-norm with iteration.

Why this matters

This approach provides a way to generate physically motivated convergence maps using **theory alone**, offering an efficient alternative to full N-body simulations. It's ideal for:

• Fast map generation across cosmologies
• Training machine learning models
• Validating pipelines or summary statistics
• Testing robustness under survey conditions

Next steps

• Extend to tomographic bins and spherical (HEALPix) geometry
• Incorporate more complex statistics like peak counts, Minkowski functionals
• Apply to real data and use in likelihood-free inference

Read the paper

👉 arXiv:2507.01707

Tinnaneri Sreekanth, V., Starck, J.-L., & Codis, S. (2025)